Measurement of coaxial cable impedance
Did you ever wonder what is
the impedance of that piece of unknown coax cable ? Well I did, but the methods
of measuring the cable impedance found on the Internet were not satisfactory
for me. So I invented a new one. Here's
how it works.
1) Take a long piece of
cable, usually 3-30 meters, the longer the better.
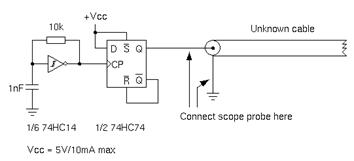
2) Connect one end of the
cable to the cca 10 ns pulser of any frequency. One can use pulser shown in Fig
2. Leave the other end of the cable open.
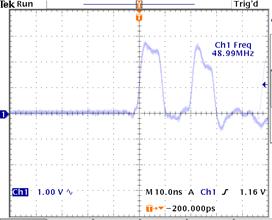
3) Measure a signal at the
driving end with a single channel scope. There will be two pulses separated by
a time lapse required for the pulse to travel down the cable AND BACK. Measure that time lapse and divide by two to
get the time DeltaT (in nanoseconds) that takes the pulse to travel down the
cable (see the Fig 1).
4) Measure the capacitance
of that particular piece of cable, C (in picofarads).
Now, the impedance of the
cable is given by:
Z = 1000 * DeltaT / C
where:
Z = impedance in Ohms
DeltaT = one way travel time
in ns through the cable
C = capacitance of the cable
in pF
Well,
the formula is simple, you dont need to know the length of the cable, you only
need to access one end of the cable, you only need one channel scope. The bad
news is that you do need a scope, a capacitancemeter and a trivial pulse
generator, but if you do not have this, you are in trouble already :-)
Measuring
a cca 2 meter long piece of RG 58 A/U gives me 52.6 Ohm, good enough for such a
short cable. Measurement of cca 29m long piece of RG174C17 50 Ohm cable (see
Fig. 3) gave Deltat = 153ns, C=3.10nF => Z=49.4 Ohm. Note that the pulses
are separated by 306ns, from which I have calculated DeltaT = 306ns/2 = 153ns. Note
also that longer cable will yield a smaller reflected pulse.
NOTE 1.
This formula might work only for coaxial cables !
NOTE 2. To
derive the formula I have used:
n = c/v = DeltaT/L=
sqrt(epsilon_r * mu_r)
where n = refraction index,
v = speed of EM waves in the isolator,
mu_r = 1 because we do not have magnetic medium.
cylindrical_capacitor_capacitance
= 2 * Pi * epsilon_0 * epsilon_r * L / ln(D/d)
epsilon_0 = 8.8542E-12
Farad/meter, vacuum dielectric constant
Z = 138 * log(D/d) /
sqrt(epsilon_r) = 59.93* ln(D/d) / n, a fromula from the book published by Howard W. Sams
& Co. 1975, page 24-21
|
Fig. 1. Original
and reflected pulses for a 2 meter long coax cable |
Fig.
2. Pulser and connection diagram |
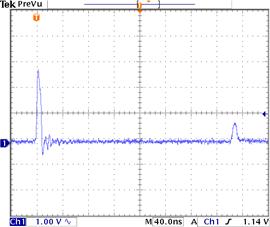
Fig. 3. .
Original and reflected pulses for a 29 meter long coax cable